Checkpoint Report

ADJUSTED NEW SCHEDULE

Nov 4 - Nov 16

Nov 16 - Nov 23

Nov 23 - Nov 30

Nov 30 - Dec 4

Dec 4 - Dec 7

Dec 7 - Dec 9

Dec 9 - Dec 14

REPORT BODY

Progress

The project began with defining the Cube representation. We opted for six 3x3 array of “COLOR”s, which is the simplest representation we could think of. The concerns for storing unnecessary COLORS were not addressed directly here, since we were aware that the Iterative Deepening A* (IDA) algorithm is a memory constrained A* algorithm. Together with this first definition of a Cube struct, a BFS solver was introduced to understand the amount of memory consumed, and provide a solution checker for the more complicated algorithms. On GHC machines, given our naive BFS implementation, the BFS solver would be killed when searching at depth 7 of the tree with a branching factor of 18. (There are 18 transitions for a Rubiks Cube at each state; although some could be pruned, optimization were no implemented at this stage)

Next, we implemented the IDA Solver. Although not much speed up over the BFS solver was observed. The new algorithm did alleviate the problem of memory consumption. We were able to resolve problems with solutions of depth 9 using this solver.

Finally, we bridged our IDA Solver with a database implementaion adapted from github and created the IDA with Korf DB (IDAKDB) solver. This solver is also parallelized using OMP and becomes the Parallel IDAKDB (ParaIDAKDB) solver. With the ParaIDAKDB solver and 16 threads, depth 11 case can be solved in 25s without any search tree branch pruning. (With the initial BFS Solver, 14s is required to solve a depth 6 case.)

Challenges

Efficient Database

To our best understanding, the most unexpected challenge is towards building the database. We were stuck for a few days. Recall the six 3x3 array of “COLOR”s representations of the cube, which unsurprisingly is very inefficient as storage for the Korf DB. We were experimenting with other cube representations; however, the amount of work to find a good enough representation and correctly generate a heuristics database was beyond expectation. Therefore, we adapted an efficient database implementation from github. (Note that only the database reader code and the generated database data files are used. The repo also contains a sequential solver, which we did not reference.)

We made the decision to adapt the database mainly because we analyzed that the heuristic bound picking process is a fixed process, i.e. reading generated data from a database. This process is not interesting from the perspective of parallelizing the solver. Although we still consider the process of generating these data challenging, for solving a Rubik’s cube case, reading from a piece of read-only memory does not make parallelization hard. (Dynamic caching is currently not part of our implementation; it may become relevant when we explore the pruning techniques. Note that dynamic caching imposes the problem of memory constraints, which was alleviated by using IDA.)

Iterative Search and Synchronization

Although the computation structure of solving a Rubik’s Cube is similar to the Wandering Sales Person tree traversal problem, the search for Rubik’s Cube imposes a few different challenges, most notably:

We plan to spend a day or two to study the implication towards parallelization of this iterative nature (besides the obvious synchronization challenges).

Preliminary Results

The speedups we measured for the ParaIDAKDB solver were (without any pruning):

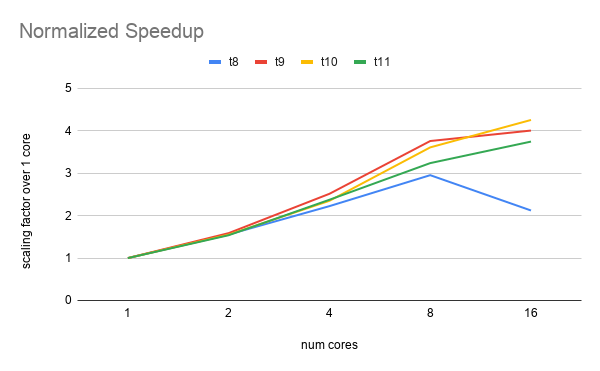
Each line is for one generated test case: “ti” case is a case where solution depth is i. So the above diagram shows measurements for test cases with solution depths from 8 through 11.

Here is a brief analysis:

Goals and Deliverables

Although not finished, the process of developing the database inspired many branch pruning ideas. This is a good side effect that we believe will eventually help us finish the project on time (together with the slack in the last week which we intentionally left open for situations like this). This process also provided insights into solvers for more generalized Rubiks Cubes. These solvers will not be implemented since they require database changes and regenerating the data. However, we will attempt to discuss these insights in the final report.

During the poster session, our goal is to perform live demo with scrambles of, say, 50 steps (whose solution must have reasonable depth) and solve it optimally according to the move sequence generated by our solver. We will also show graphs to demonstrate speedups we achieved with different pruning techniques.

Change to Old Goals

Due to database challenges, and its uninteresting nature for parallelization, we propose to switch the old goal of implementing solver for NxNxN cube into the new goal proposed below. The NxNxN cube solver requires changing database encodings and regenerating the database for heuristics.

Additional New Goals

As an additional goal, we plan to parallelize the solver with MPI (besides OMP). We expect to have time to implement these two once our experiments with branch pruning ideas are complete.

References